Chapitre 9 : Application linéaire

1. Aparté d’analyse

Une fonction de l’ensemble $X$ à l’ensemble $Y$ est une règle qui dit comment les éléments de deux ensembles sont associés.

On appelle image, l’élément $y \in Y$ qui est associé à un $x \in X$ par la fonction. On appelle préimage, l’élément $x \in X$ qui est associé à un $y \in Y$ par la fonction.

Exemple I

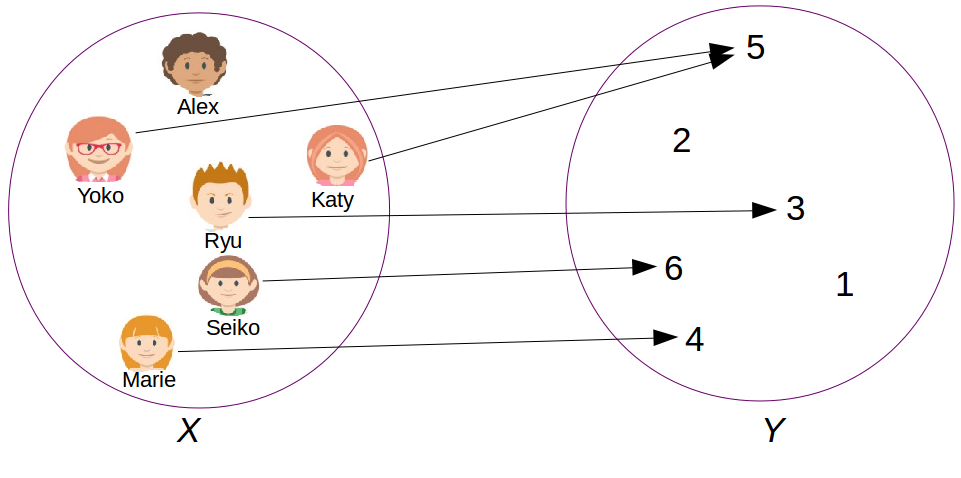
La fonction représentée à la Figure 9.1 associe les notes qu’ont obtenues les élèves de la classe D1 lors dernier test de statistiques. On a :

• $X=\{\text{Alex}, \text{Marie}, \text{Yoko}, \text{Ryu}, \text{Seiko}, \text{Katy}\}$. $Y=\{1,2,3,4,5,6\}$.
• L’image de $\text{Marie}$ par la fonction est $4$.
• La préimage de $5$ par la fonction est $\{\text{Yoko}, \text{Katy}\}$.
• $\text{Alex}$ n’a pas d’image (pas présent lors du test).
• $1$ et $2$ n’ont pas de préimage.

Figure 9.1 : fonction

2. Définition

Une application linéaire ou transformation linéaire est une fonction qui satisfait les deux conditions suivantes :

En d’autres termes, cela signifie que l’ordre du traitement est égal. On peut soit effectuer d’abord l’opération arithmétique (addition ou multiplication) et ensuite appliquer le résultat à la fonction, ou l’inverse. Les deux sont équivalents.

Exemple II

Soit la fonction $j$ :

$$\begin{equation} j \colon \, \mathbb{R} \to \mathbb{R} \tag{3} \\ \quad x \mapsto 3x \end{equation}$$

$(3)$ est une application linéaire car satisfait $(1)$ et $(2)$ :

$$\eqalignno{ j(a + b) &= 3(a+b) = \underbrace{3a}_{j(a)} + \underbrace{3b}_{j(b)} &(4) \cr j(\lambda a) &= 3(\lambda a) = \lambda \underbrace{3a}_{j(a)} & (5)\cr }$$

Exemple III

Soit la fonction $k$:

$$\begin{equation} k \colon \, \mathbb{R} \to \mathbb{R} \tag{6} \\ \quad x \mapsto -2x +9 \end{equation}$$

$(6)$ n’est pas une application linéaire car ne satisfait ni $(1)$ ni $(2)$ :

$$\eqalignno{ k(a + b) &= -2(a+b)+9 = -2a -2b+9 \ne \underbrace{-2a+9}_{k(a)} + \underbrace{-2b+9}_{k(b)} &(7) \cr k(\lambda a) &= -2(\lambda a)+9 \ne \lambda ( \underbrace{-2a+9}_{k(a)} ) & (8) \cr }$$

3. Matrice et application linéaire

Sur la base des propriétés des opérations sur matrices, on peut montrer en effet que :

$$\begin{equation} A(\vec{a}+ \vec{b}) = A\vec{a}+ A\vec{b} \tag{9} \end{equation}$$

$$\begin{equation} A(\lambda \vec{a}) = \lambda A\vec{a} \tag{10} \end{equation}$$

Une matrice multipliant un vecteur satisfait les conditions $(1)$ et $(2)$ et ainsi décrit une application linéaire.

4 .Concrètement ?

Les applications linéaires sont par exemple utilisées pour faire des manipulations d’images ou des rotations d’objets dans les jeux vidéos.

Exemple IV

Soit l’application linéaire $l$ :

$$\begin{equation} l \colon \, \mathbb{R}^2 \to \mathbb{R}^2 \\ \left( \begin{smallmatrix} x_1 \\ x_2 \end{smallmatrix} \right) \mapsto \left( \begin{smallmatrix} 3 & 0 \\ 0 & 2 \end{smallmatrix} \right) \left( \begin{smallmatrix} x_1 \\ x_2 \end{smallmatrix} \right) \tag{11} \end{equation}$$

La figure 9.2 montre en pointillé la transformation que subit une forme par l’application. La transformation est un étirement.

Figure 9.2 : transformation linéaire

Figure 9.3 : transformation linéaire personnalisée (credits Disney-Pixar)

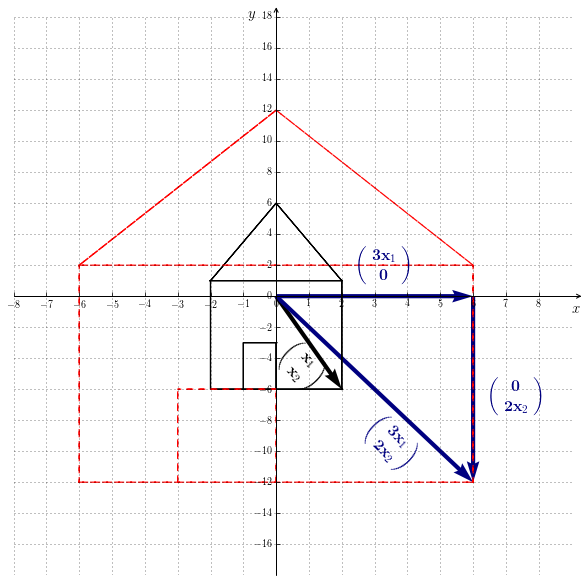
Définis une application linéaire de ton choix et observe le résultat !

Récapitulation