1. Analytical aside
A function from a set $X$ to a set $Y$ is rule telling how elements of both sets are associated each other.
The element $y \in Y$ associated, under the function, to the element $x \in X$ is the so-called image.
The element $x \in X$ associated, under the function, to the element $y \in Y$ is the so-called pre-image.
Example I
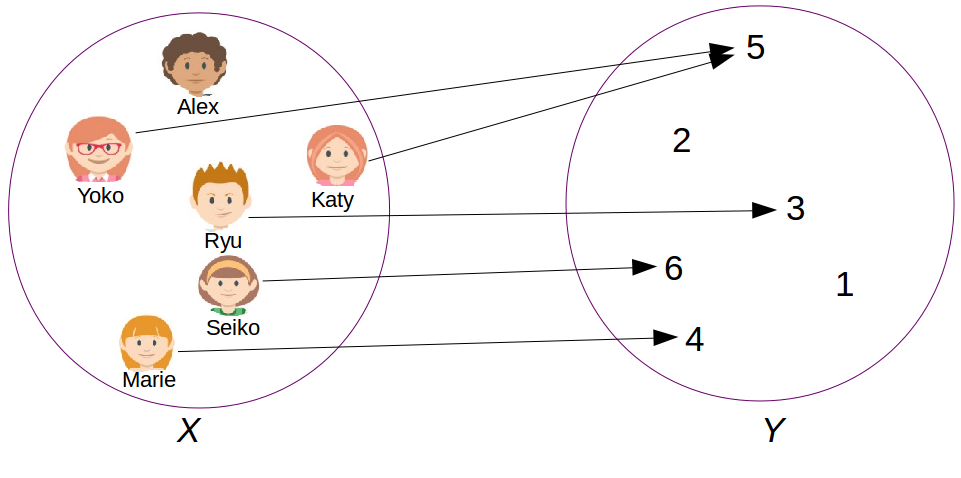
The function represented in Figure 9.1 associates the grades of the students belonging to the class D1 in respect to the last examination of statistics. We have :
- $X= \{\text{Alex}, \text{Marie}, \text{Yoko}, \text{Ryu}, \text{Seiko}, \text{Katy}\}$. $Y=\{1,2,3,4,5,6\}$.
- The image of $\text{Marie}$ under the function is $4$.
- The pre-image of $5$ under the function is $\{\text{Yoko}, \text{Katy}\}$.
- $\text{Alex}$ does not have any image (absent at the examination).
- $1$ and $2$ both do not have any pre-image.
2. Definition
A linear mapping or linear transformation is a function satisfying the two following conditions:
In other words, for a linear transformation the order things are processed does dot matter. You can either first proceed the arithmetic operation (multiplication or addition) and second apply the result to the function, or reversely. Both leads to the same result.
Example II
Let $j$ :
$(3)$ is a linear transformation since $(1)$ and $(2)$ both are satisfied :
Example III
Let $k$ :
$(6)$ is not a linear transformation since neither $(1)$ nor $(2)$ are satisfied :
3. Matrix and linear transformation
Based on the properties of the matrices operations, it can be shown that :
A matrix multiplying a vector satisfies the two conditions $(1)$ and $(2)$ and is thus a linear transformation.
4. But more concretely ?
Linear transformations are for example used in image processing or for making objects rotate in video games.
Example IV
Let $l$ :
In Figure 9.2 is illustrates in dashed line the linear transformation of a shape. The transformation is in that case a stretching.
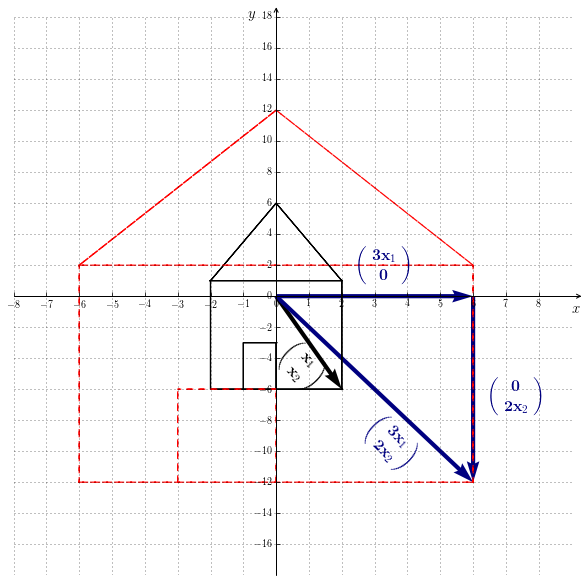

Let’s define a linear transformation of your own and observe the result !
Recapitulation
A matrix multiplying a vector is a linear transformation (also called linear mapping).
This kind of mapping stretches (or shrinks) a vector or rotates a vector or combines both.