studybyyourself » Chapitre 7 : Déterminant

La théorie des déterminants est un vaste sujet et nous allons les aborder que dans un cadre limité.

Le déterminant permet de répondre de manière rapide à la question de la dépendance linéaire de vecteurs.

1. Calcul

Le déterminant d’ordre 1 se calcule de la manière suivante :

$\begin{equation} \begin{vmatrix} a \\ \end{vmatrix} = a \end{equation}$

Le déterminant d’ordre 2 se calcule de la manière suivante :

$\begin{equation} \begin{vmatrix} a & c \\ b & d \end{vmatrix} = ad -bc \end{equation}$

Le déterminant d’ordre 3 se calcule de la manière suivante :

$\begin{equation} \begin{vmatrix} a & d & g \\ b & e & h \\ c & f & i \\ \end{vmatrix} = a\, \begin{vmatrix} e & h \\ f & i \end{vmatrix} -b\, \begin{vmatrix} d & g \\ f & i \end{vmatrix} +c\, \begin{vmatrix} d & g \\ e & h \end{vmatrix} \end{equation}$

Le calcul du déterminant d’ordre supérieur à trois sort du cadre du présent cours. Voir ici pour les interessés.

2. Test de dépendance

Le test de dépendance se fait à l’aide de la propriété suivante des déterminants :

$\begin{equation} \det(\vec{v_1}, \cdots, \vec{v_n} ) = 0 \iff \text{les vecteurs sont linéairement} \, \textbf{dépendants} \end{equation}$

Par la contraposée de $(4)$, on a :

$\begin{equation} \det(\vec{v_1}, \cdots, \vec{v_n} ) \neq 0 \iff \text{les vecteurs sont linéairement} \, \textbf{indépendants} \end{equation}$

Exemple I

Testons la dépendance linéaire des vecteurs suivants : $ \left(\begin{smallmatrix} 8 \\ -4 \\ -3 \end{smallmatrix}\right), \left( \begin{smallmatrix} 2 \\ -4 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} -2 \\ 0 \\ 1 \end{smallmatrix} \right)$

$\begin{equation} \begin{split} \begin{vmatrix} 8 & 2 & -2 \\ -4 & -4 & 0 \\ -3 & 0 & 1 \\ \end{vmatrix} & = 8 \, \begin{vmatrix} -4 & 0 \\ 0 & 1 \end{vmatrix} -(-4) \, \begin{vmatrix} 2 & -2 \\ 0 & 1 \end{vmatrix} +-3 \, \begin{vmatrix} 2 & -2 \\ -4 & 0 \end{vmatrix} \\ & = 8\,(-4 \cdot 1 - 0 \cdot 0) + 4\,(2\cdot 1 - 0 \cdot -2) -3\,(2\cdot 0 - -4 \cdot -2) \\ & = 8\,(-4) + 4\,(2) -3\,( -8) \\ & =-36 + 8 + 24 \\ & = 0 \end{split} \end{equation}$

Conformément à $(4)$, les vecteurs sont linéairement dépendants.

3. Concrètement ?

En quoi le calcul du déterminant renseigne sur la dépendance linéaire de vecteurs ?

Figure 7.1 : aire d’un parallèlogramme (wikipedia)

Figure 7.2 : volume d’un parallélépipède (wikipedia)

En fait, le déterminant donne l’aire du parallélogramme formé par deux vecteurs de $\mathbb{R}^2$ (Figure 7.1), respectivement le volume du parallélépipède que forment trois vecteurs de $\mathbb{R}^3$ (Figure 7.2).

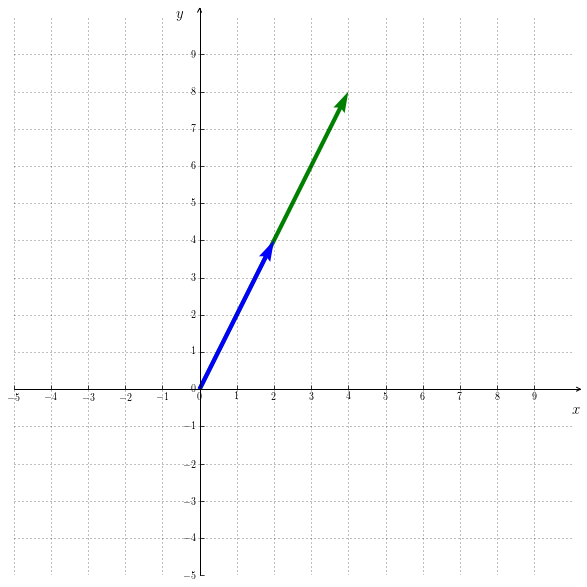
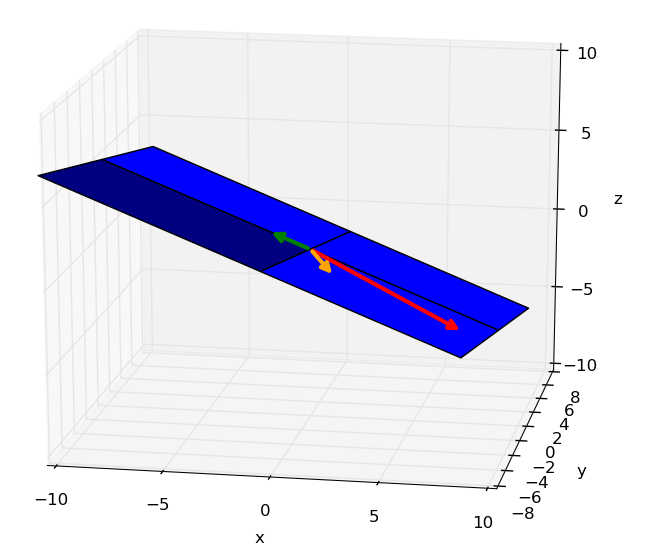
La Figure 7.3 illustre le segment formé par deux vecteurs linéairement dépendants de $\mathbb{R}^2$. L’aire est de $0$ puisqu’on a pas de largeur. La Figure 7.4 illustre le même principe dans $\mathbb{R}^3$. Sans hauteur, on a un volume nul.

Figure 7.3 : aire nulle

Figure 7.4 : volume nul

Récapitulation

Le déterminant de vecteurs permet de tester, de manière rapide, si ces vecteurs sont linéairement dépendants ou pas.

Le déterminant donne (en valeur absolue) l’aire que forment deux vecteurs de $\mathbb{R}^2$, respectivement le volume que forment trois vecteurs de $\mathbb{R}^3$. D’une manière générale, le déterminant donne l’hypervolume de l’hyperparallélépipède formé par $n$ vecteurs de $\mathbb{R}^n$.

Si les vecteurs sont linéairement dépendants alors le déterminant vaut $0$.