The theory determinant is a vast topic, so we won’t dive too much into it here.
The derterminant can be used for quickly testing whether a set of vectors are linearly dependent.
1. Calculation
The calculation of determinant of order 1 proceeds as follows :
The calculation of determinant of order 2 proceeds as follows :
The calculation of determinant of order 3 proceeds as follows :
The calculation of determinant of order higher than 3 is beyond the scope of the this course. Please refer here if you want to know more about it.
2. Dependence test
The test of linear dependence is done by using the following property of determinants :
The contraposition of $(4)$ gives :
Example I
Let’s test the linear dependence of the following vectors : $ \left(\begin{smallmatrix} 8 \\ -4 \\ -3 \end{smallmatrix}\right), \left( \begin{smallmatrix} 2 \\ -4 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} -2 \\ 0 \\ 1 \end{smallmatrix} \right)$
According to $(4)$ the vetors are linearly dependent.
3. But more concretely ?
How does the determinant help telling about the linear dependance of vectors ?


The determinant actually gives the area of the parallelogram that two vectors of $\mathbb{R}^2$ (Figure 7.1) form together, respectively the volume of the parallelepiped that three vectors of $\mathbb{R}^3$ form togheter (Figure 7.2).
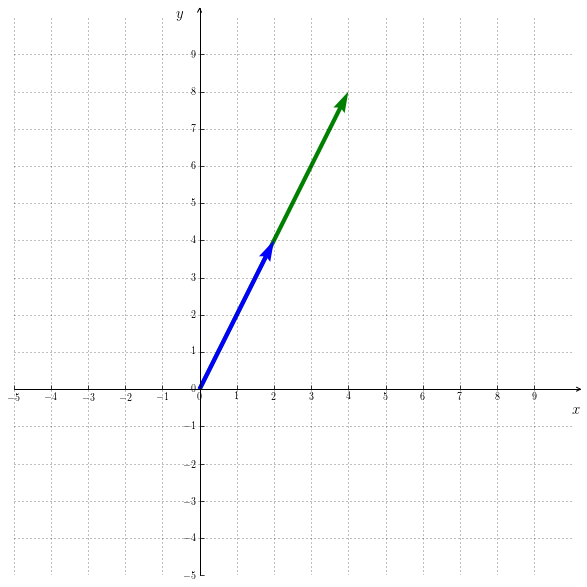
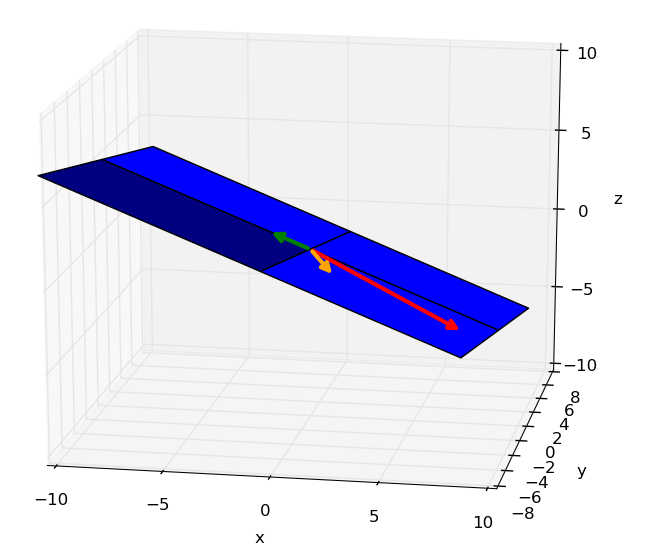
Figure 7.3 illustrates the line segment that two linearly dependent vectors of $\mathbb{R}^2$ form together. Since that one has no width, the area is equal to $0$. Figure 7.4 illustrates the same idea in $\mathbb{R}^3$. Without any height the volume equals $0$.
Recapitulation
Determinant of vectors can be used for quickly testing whether those vectors are linearly dependent or not.
The determinant gives (in absolute value) the area of the parallelogram that two vectors of $\mathbb{R}^2$ form together, respectively the volume of the parallelepided that three vectors of $\mathbb{R}^3$ form together. More generally, the determinant gives the hypervolume of the hyperparallelepiped that $n$ vectors of $\mathbb{R}^n$ form together.
If a set of vectors are linearly dependent, then their determinant equals $0$.