Chapitre 4 : signature numérique

1. But

La signature numérique rempli en fait un double but. Premièrement, elle sert à être certain qu’un texte ou document n’a pas été modifié durant son transport. On appelle cela l’intégrité d’un document. Deuxièmement, l’identité de l’émetter peut être véfifiée. Cette caractéristique s’appelle l’authentification.

2. Hash

Avant de voir comment fonctionne la signature numérique, il faut savoir que celle-ci utilise la notion de hash qui est un concept indépendant.

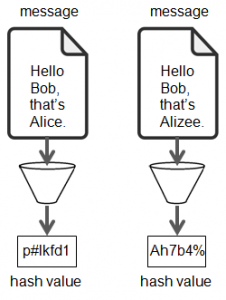
Un hash est le condensé ou résumé d’une information (p.ex. texte ou document). Pour l’obtenir, on prend l’information comme input (entrée) et on lui applique une fonction mathématique. On appelle cette fonction la fonction de hachage et son output (valeur de sortie) est appelé le hash (voir Figure 4.1). Appliquons par exemple, le texte Hello Bob, that's Alice. à une à fonction de hachage arbitraire $f$. Nous obtenons le hash de la façon suivante :
$$f(\text{Hello Bob, that’s Alice.})=\text{p#lkfd1}$$

La fonction de hachage est une fonction qui doit remplir plusieurs propriétés mathématiques. Nous mentionnerons ici simplement qu’elle est une fonction à sens unique. En effet, connaissant l’output et la fonction de hachage, il est impossible de connaître l’input.

Parmi les nombreuses fonction de hachage, citons MD5 (n’est plus sûr), SHA-3, etc.

Figure 4.1 : Inputs assez proches produisent des hashs très différents

3. Signature numérique = hash chiffré

Au message initial on ajoute un hash de celui-ci. Ce hash est chiffré avec la clé privée de l’émetteur. Cela constitue la signature numérique.

4. Illustration

Figure 4.2 : Processus de la signature numérique

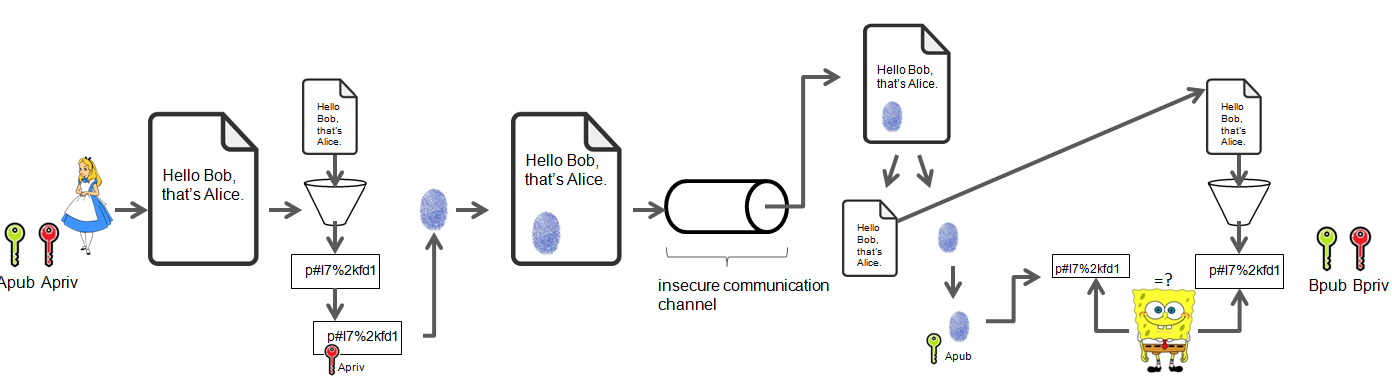
1. Alice écrit le message suivant à Bob : Hello Bob, that's Alice.. Elle applique celui-ci à une fonction de hachage et obtient le hash. Elle chiffre le hash avec sa clé privée. Finalement, elle joint le hash chiffré (signature) au message et envoie le tout à Bob.
2. A réception, Bob sépare le message et la signature. Il déchiffre la signature avec la clé publique d’Alice. Ensuite, il applique le message à la fonction de hachage. Il obtient un autre hash. Il compare les deux hashs. Si les deux hashs sont identiques alors le message initial n’a pas été modifié en route. Evidemment, Bob devra utiliser le même chiffre et la même fonction de hachage qu’Alice.

La signature numérique garanti donc :

1. Intégrité : Si le message initial est modifié en cours de route, les hashs ne correponderont pas.
2. Authentification : Si la signature est falsifiée en cours de route, les hashs ne corresponderont pas.

6. Inconvéninent majeur

Supposons maintenant que l’on chiffre le tout (message + signature) avec la clé publique du destinataire et qu’on le lui envoie, comme on l’a vu dans le chapitre de la cryptographie asymétrique. Le destinaire déchiffrera le tout avec sa clé privée et vérifiera si les hashs correspondent.

Malheureusement, le problème de l’attaque MITM n’est pas toujours pas résolu. En effet, en détournant la communication dans les deux sens comme on l’a vu précédemment, MITM peut toujours déchiffrer les messages. Le certificat numérique résout définitivement ce problème.