studybyyourself » Chapitre 11 : Valeurs propres et vecteurs propres

1. Définition

Nous avons vu qu’une matrice $A$ qui multiplie un vecteur $\vec{x}$ est en réalité une application linéaire.

On s’intéresse maintenant au vecteur $\vec{x}$ dont l’image $\vec{y}$ (par l’application) est linéairement dépendante de lui-même, à savoir :

$\begin{equation} \underbrace{ A\vec{x} }_{ \vec{y} } = \lambda \vec{x} \qquad (\vec{x} \neq \vec{0} ) \end{equation}$

Les $\lambda$ et $\vec{x}$ qui satisfont $(1)$ sont appelés respectivement valeurs propres et vecteurs propres.

Dans $(1)$ on a exclu $\boldsymbol{\vec{0}}$ . On sait en effet de toute façon que $\underbrace{A\,\vec{0}}_{ \vec{0} } = \underbrace{ \lambda\, \vec{0} }_{ \vec{0} } \,$ est vrai quel que soit $\lambda$ .

2. Calcul

De $(1)$ on a :

$\begin{equation} A\vec{x} = \lambda \vec{x} \iff A\vec{x}-\lambda \vec{x} = \vec{0} \iff (A -\lambda I)\,\vec{x} = \vec{0} \end{equation}$

$\begin{equation} \iff \left[ \left( \begin{array}{} a_{1,1} & \cdots & a_{1,n} \\ \phantom{1} \vdots & a_{i,i} & \phantom{1}\vdots \\ a_{n,1} & \cdots & a_{n,n} \end{array} \right) - \left( \begin{array}{} \lambda & \cdots & 0 \\ \vdots & \lambda & \vdots \\ 0 & \cdots & \lambda \end{array} \right) \right] \vec{x} = \vec{0} \end{equation}$

$\begin{equation} \iff \left( \begin{array}{} a_{1,1} -\lambda & \phantom{11} \cdots & a_{1,n} \\ \phantom{-11} \vdots & a_{i,i}-\lambda & \phantom{11}\vdots \\ \smash{ \underbrace{ a_{n,1} \phantom{1-\lambda}}_{ \vec{C_1} }} & \smash{ \underbrace{ \phantom{11} \cdots \phantom{1 \lambda} }_{ \vec{C_i} }} & \smash{ \underbrace{a_{n,n}-\lambda \phantom{1} }_{ \vec{Cn} }} \end{array} \right)\vec{x} = \vec{0} \end{equation}$

$\begin{equation} \iff x_1 \vec{C_1} + \cdots + x_i \vec{C_i} + \cdots + x_n\vec{C_n} = \vec{0} \end{equation}$

En $(5)$ on a decomposé la multiplication matrice par vecteur de $(4)$ . Les colonnes $\vec{C_1}, \dots, \vec{C_n}$ doivent être linéairement dépendantes car les $x_i$ ne peuvent être nuls à cause de $(1)$ . Ceci implique que leur déterminant est nul.

Une fois les $\lambda$ ’s (valeurs propres) trouvés par le biais du déterminant on remplace leur valeur dans la matrice de $(4)$ pour trouver les vecteurs propres y relatif.

Exemple I

Soit $h$ : $h \colon \, \mathbb{R}^2 \to \mathbb{R}^2$ , $\vec{x} \mapsto \left( \begin{smallmatrix} 2 & 1 \\ 3 & 4 \end{smallmatrix} \right) \vec{x}$ .
Calculons ses valeurs et vecteurs propres.

De $(4)$ on a :

$\begin{equation} \left( \begin{array}{} 2-\lambda & 1 \\ 3 & 4-\lambda \end{array} \right) \vec{x} = \vec{0} \end{equation}$

Les colonnes de la matrice de $(6)$ sont linéairement dépendantes, donc :

$\begin{equation} \begin{split} \begin{vmatrix} 2-\lambda & 1 \\ 3 & 4 -\lambda \\ \end{vmatrix} & = (2-\lambda)(4 -\lambda) -3 \\ & =8 - 2\lambda - 4\lambda +\lambda^2 -3 \\ & = \lambda^2 - 6\lambda + 5 \\ & = (\lambda-1)(\lambda-5) \\ & = 0 \end{split} \end{equation}$

On en conclu de $(7)$ : $\lambda_1 =1$ et $\lambda_2 =5$

Pour déterminer le vecteur propre $\vec{x}_1$ associé à $\lambda_1$ , on remplace $\lambda_1$ dans $(6)$ :

$\begin{equation} \left( \begin{array}{} 2-1 & 1 \\ 3 & 4-1 \end{array} \right) \vec{x}_1 = \vec{0} \iff \left( \begin{array}{} 1 & 1 \\ 3 & 3 \end{array} \right) \vec{x}_1 = \vec{0} \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} 1 & 1 & 0 \\ 3 & 3 & 0 \end{array} \right) \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} 1 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \end{equation}$

$\iff 1x+1y = 0 \iff x=-y$ . On pose $x= \beta$ .

$\begin{equation} \vec{x}_1 = \begin{pmatrix} \beta \\ -\beta \end{pmatrix} \end{equation} \iff \vec{x}_1 = \beta \begin{pmatrix} 1 \\ -1 \end{pmatrix} ,\quad \beta \in \mathbb{R}_{ \ne 0}$

Pour déterminer le vecteur propre $\vec{x}_2$ associé à $\lambda_2$ , on remplace $\lambda_2$ dans $(6)$ :

$\begin{equation} \left( \begin{array}{} 2-5 & 1 \\ 3 & 4-5 \end{array} \right) \vec{x}_2 = \vec{0} \iff \left( \begin{array}{} -3 & 1 \\ 3 & -1 \end{array} \right) \vec{x}_2 = \vec{0} \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} -3 & 1 & 0 \\ 3 & -1 & 0 \end{array} \right) \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} -3 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \end{equation}$

$\iff -3x+1y = 0 \iff y=3x \iff x=\frac{y}{3}$ . On pose $x= \beta$ .

$\begin{equation} \vec{x}_2 = \begin{pmatrix} \beta \\ 3\beta \end{pmatrix} \end{equation} \iff \vec{x}_2 = \beta \begin{pmatrix} 1 \\ 3 \end{pmatrix} ,\quad \beta \in \mathbb{R}_{ \ne 0}$

3. Concrètement ?

Figure 10.1 : vecteur propre et vecteur ordinaire

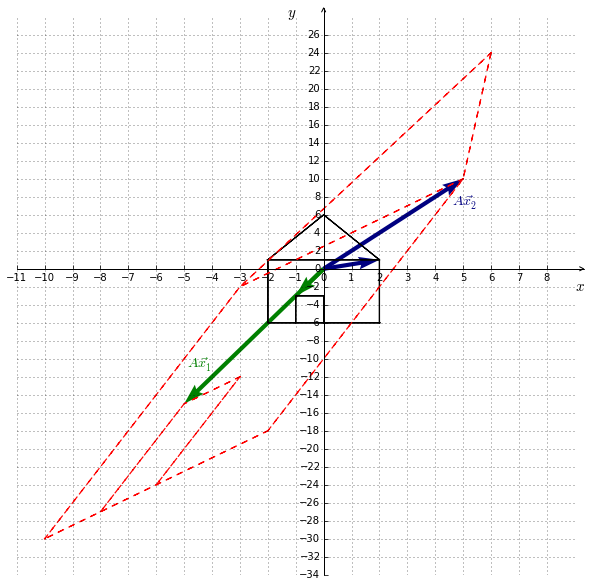
La figure 10.1 illustre une forme avant et après transformation (en pointillé) par l’application de l’exemple I.

Un vecteur propre $\,\color{green}{\vec{x_1}}=\left(\begin{smallmatrix} -1 \\ -3 \end{smallmatrix}\right)$ , ainsi qu’un vecteur ordinaire $\color{navy}{\vec{x_2}}=\left(\begin{smallmatrix} 2 \\ 1 \end{smallmatrix}\right)$ sont également représentés. On peut voir que le vecteur propre ne subit pas de rotation par l’application.

Récapitulation

Un vecteur propre est un vecteur dont l’image (par l’application) est linéairement dépendante de lui-même, à savoir $\underbrace{ A\vec{x} }_{ \vec{y} } = \lambda \vec{x}$ .

D’abord on trouve les valeurs propres en résolvant le polynôme caractéristique et ensuite on peut trouver les vecteurs propres qui y sont associés.

Le polynôme caractéristique s’obtient en calculant le déterminant de la matrice $A -\lambda I$ .

Par définition, un vecteur propre ne doit pas être égal au vecteur nul.