studybyyourself » Chapitre 8 : Base

1. Analogie

De manière générale, une base est un système de référence dans lequel les objets sont exprimés. Par exemple, le nombre $64$ s’écrit 1000 en base $2$ (base binaire). Il s’agit en fait des mêmes nombres mais exprimés (représentés) dans des bases différentes :

$\begin{equation} 64_{10} = 1000_{2} \end{equation}$

La base naturelle pour les nombres est la base $10$ . Pour les vecteurs, la base naturelle est appelée la base standard (aussi appellée base canonique ou base normale).

2. Représentations

Tout comme les nombres, les vecteurs sont représentés par rapport à une base.

Exemple I

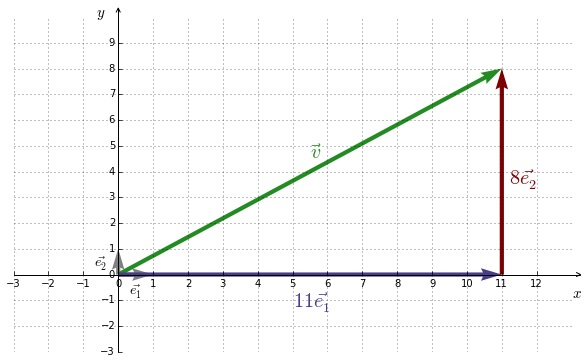
La figure 8.1 montre le vecteur $\vec{v}= \left( \begin{smallmatrix} 11 \\ 8 \end{smallmatrix} \right)$ représenté dans la base standard de $\mathbb{R}^2$ , soit $STD = \{ \underbrace{\left( \begin{smallmatrix} 1 \\ 0 \end{smallmatrix} \right)}_\vec{e_1}, \underbrace{\left( \begin{smallmatrix} 0 \\ 1 \end{smallmatrix} \right)}_\vec{e_2} \}$ .

En réalité, $\vec{v}$ est issu d’une combinaison linéaire des vecteurs de sa base :

$\begin{equation} \vec{v} = 11 \underbrace{\begin{pmatrix} 1 \\ 0 \end{pmatrix}}_{\vec{e_1}} + 8 \underbrace{\begin{pmatrix} 0 \\ 1 \end{pmatrix}}_{\vec{e_2}} = \begin{pmatrix} 11 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 8 \end{pmatrix} = \begin{pmatrix} 11 \\ 8 \end{pmatrix} \end{equation}$

Figure 8.1 :

$\vec{v}$ dans la base base standard de

$\mathbb{R}^2$

Figure 8.2 :

$\vec{v}$ dans une base quelconque

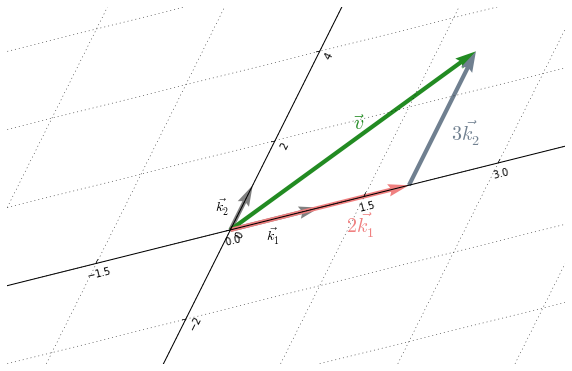
Représentons $\vec{v}$ dans une autre base de $\mathbb{R}^2$ , soit la base $B= \{ \underbrace{ \left( \begin{smallmatrix} 4 \\ 1 \end{smallmatrix} \right)}_{\vec{k_1}}, \underbrace{ \left( \begin{smallmatrix} 1 \\ 2 \end{smallmatrix} \right) }_{\vec{k_2}} \}$ .

On doit donc résoudre l’équation suivante :

$\begin{equation} \vec{v} =\begin{pmatrix} 11 \\ 8 \end{pmatrix} = \lambda_1\vec{k_1} +\lambda_2\vec{k_2} = \lambda_1 \begin{pmatrix} 4 \\ 1 \end{pmatrix} + \lambda_2 \begin{pmatrix} 1 \\ 2 \end{pmatrix} \end{equation}$

Dans $(3)$ les coefficients $\lambda_i$ sont appelés les composantes (ou coordonnées). En résolvant $(3)$ on obtient $2$ et $3$ comme composante de $\vec{v}$ dans $B$ .

La figure 8.2 illustre $\vec{v}$ dans $B$ .

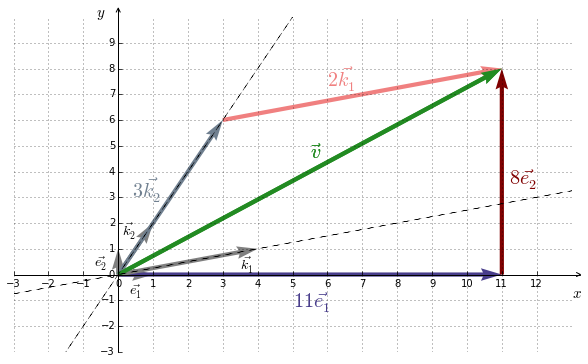
On a donc un vecteur $\vec{v}$ représenté dans deux bases différentes :

$\begin{equation} \begin{pmatrix} 11 \\ 8 \end{pmatrix}_{STD} =\begin{pmatrix} 2 \\ 3 \end{pmatrix}_{B} \end{equation}$

Figure 8.3 :

$\vec{v}$ dans deux bases

3. Conditions

Une base doit remplir les conditions suivantes :

N’importe quel vecteur d’un espace donné doit pouvoir être construit par combinaison linéaire de la base. C’est le but d’une base.
Les vecteurs d’une base doivent être linéairement indépendants.

4. Changement de base

Pour convertir un vecteur d’une base $B$ à la base standard on peut utiliser la formule suivante :

$\begin{equation} B \cdot \vec{v}_{B}= \vec{v}_{STD} \end{equation}$

Exemple II

Convertir $\vec{v}=\left( \begin{smallmatrix} 2 \\ 3 \end{smallmatrix} \right)$ de la base $B=\{\left( \begin{smallmatrix} 4 \\ 1 \end{smallmatrix} \right),\left( \begin{smallmatrix} 1 \\ 2 \end{smallmatrix} \right)\}$ , à la base standard.

$\begin{equation} \begin{pmatrix} 4 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 11 \\ 8 \end{pmatrix} \end{equation}$

Récapitulation

Tout vecteur s’exprime par rapport à une base donnée. Par défaut, un vecteur est exprimé dans la base standard.

La base standard de l’espace $\mathbb{R}^{2}$ est $\{ \left( \begin{smallmatrix} 1 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} 0 \\ 1 \end{smallmatrix} \right) \}$ . La base standard de l’espace $\mathbb{R}^{3}$ est $\{ \left( \begin{smallmatrix} 1 \\ 0 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} 0 \\ 1 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} 0 \\ 0 \\ 1 \end{smallmatrix} \right) \}$ .

Une base d’un espace donné permet de construire, par combinaison linéaire, n’importe quel élément de cet espace.

On appelle les composantes (ou coordonées) d’un vecteur, la représentation d’un vecteur dans une base donnée.

Toutes les bases de $\mathbb{R}^{2}$ contiennent $2$ vecteurs, toutes les bases de $\mathbb{R}^{3}$ contiennent $3$ vecteurs, etc. De manière générale, toutes les bases de $\mathbb{R}^{n}$ contiennent $n$ vecteurs.