studybyyourself » Chapitre 6 : Dépendance linéaire

1. Combinaison linéaire

Si un vecteur peut être exprimé par une combinaison linéaire d’autres vecteurs, on dit qu’ils sont linéairement dépendants.

Exemple I

Figure 6.1 : vecteurs linéairement dépendants

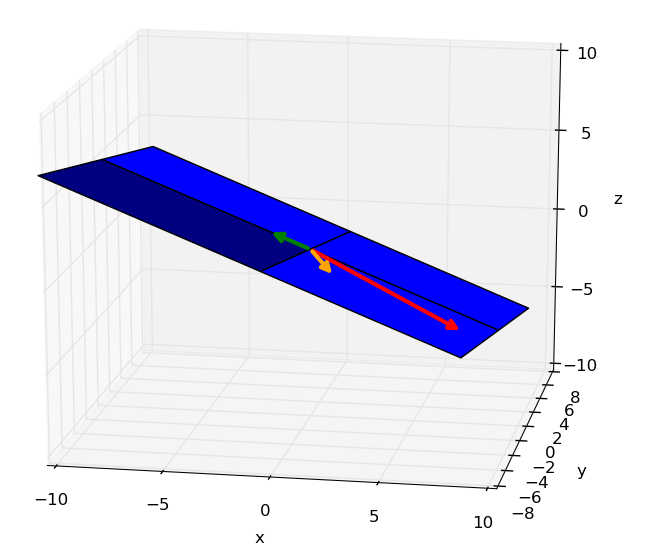
Nous aimerions savoir si un vecteur de la Figure 6.1 peut être exprimé en fonction des autres, comme suit :

$\begin{equation} \vec{v_1} = \lambda{_2} \vec{v_2} + \lambda{_3} \vec{v_3} \end{equation}$

On a donc :

$\begin{equation} \underbrace{ \begin{pmatrix} 8 \\ -4 \\ -3 \end{pmatrix}}_{\color{red}{\vec{v_1}}} = \lambda{_2} \underbrace{ \begin{pmatrix} 2 \\ -4 \\ 0 \end{pmatrix}}_{\color{orange}{\vec{v_2}}} + \lambda{_3} \underbrace{ \begin{pmatrix} -2 \\ 0 \\ 1 \end{pmatrix}}_{\color{green}{\vec{v_3}}} \end{equation}$

Factorisons la partie de droite de $(2)$ :

$\begin{pmatrix} 8 \\ -4 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \lambda{_2} \\ -4 \lambda{_2} \\ 0 \lambda{_2} \end{pmatrix} + \begin{pmatrix} -2 \lambda{_3} \\ 0 \lambda{_3} \\ 1 \lambda{_3} \end{pmatrix} = \begin{pmatrix} 2 \lambda{_2} + -2 \lambda{_3} \\ -4 \lambda{_2} + 0 \lambda{_3} \\ 0 \lambda{_2} + 1 \lambda{_3} \end{pmatrix} = \begin{pmatrix} 2 & -2 \\ -4 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} \lambda{_2} \\ \lambda{_3} \end{pmatrix}$

Echelonnons maintenant la matrice augmentée comme vu au chapitre consacré:

$\left( \begin{array}{ c c| c} 2 & -2 & 8 \\ -4 & 0 & -4 \\ 0 & 1 & -3 \end{array} \right) \overset{2R{_1}+R{_2}\rightarrow{R_2}}{\iff} \left( \begin{array}{ c c | c} 2 & -2 & 8 \\ 0 & -4 & 12 \\ 0 & 1 & -3 \end{array} \right) \overset{ 4R{_3}+R{_2}\rightarrow{R_3}}{\iff} \left( \begin{array}{c c | c} 2 & -2 & 8 \\ 0 & -4 & 12 \\ 0 & 0 & 0 \end{array} \right)$

De la forme échelonnée, on a :

$ -4\lambda_3 = 12 \iff$ $\lambda_3 = -3$

On remplace $\lambda_3$ dans la première ligne :

$2\lambda_2 + -2 \cdot \underbrace{-3}_{\lambda_3} = 8 \iff$ $\lambda_2 = 1$

La solution est donc :

$\begin{equation} \vec{\lambda} = \begin{pmatrix} 1 \\ -3 \end{pmatrix} \end{equation}$

Par conséquent, n’importe quel vecteur $\vec{v_i} \in \{\vec{v_1}, \vec{v_2}, \vec{v_3}\}$ s’exprime comme la combinaison des autres.

2. Généralisation

$(1)$ est évidemment équivalent à $(4)$ :

$\begin{equation} \vec{0} = -\vec{v_1} + \lambda{_2} \vec{v_2} + \lambda{_3} \vec{v_3} \end{equation}$

De manière plus générale, on a :

$\begin{equation} \vec{0} = \lambda{_1} \vec{v_1} + \lambda{_2} \vec{v_2} + \lambda{_2} \vec{v_3} \end{equation}$

Si l’équation $(5)$ a comme unique solution $\lambda{_1}=\lambda{_2}=\lambda{_3}=0$ alors on ne peut pas exprimer un des vecteurs comme étant la combinaison des autres. Sinon les vecteurs sont linéairement dépendants.

Récapitulation

Si un vecteur peut etre exprimé comme la combinaison d’autre(s) vecteur(s), on dit qu’ils sont linéairement dépendants. Par exemple :
$\left( \begin{smallmatrix} 2 \\ -1 \\ -1 \end{smallmatrix} \right) =
{\small -1} \left( \begin{smallmatrix} 1 \\ -1 \\ 0 \end{smallmatrix} \right) +
{\small -1} \left( \begin{smallmatrix} -3 \\ 2 \\ 1 \end{smallmatrix} \right)$.

Pour savoir si un vecteur $\vec{v_i} \in \{\vec{v_1}, \vec{v_2}, \ldots{} ,\vec{v_n} \}$ peut être exprimé comme combinaison linéaire des autres, il faut résoudre l’équation :

$\vec{0} = \lambda{_1}\vec{v_1} + \lambda{_2}\vec{v_2} + \ldots{} + \lambda{_n}\vec{v_n}$

Si cette équation admet comme unique solution tous les $\lambda{_i}=0$, alors on ne peut pas exprimer un des $\vec{v_i}$ en fonction des autres. Les vecteurs sont alors linéairement indpédendants.