studybyyourself » Chapitre 5 : Vecteur

1. Définition

Géométriquement, un vecteur est une flèche qui a les trois caractéristiques suivantes :

une direction (celle de la droite qui contient le vecteur)
un sens (haut, droite, bas, gauche)
une longeur (aussi appelé norme)

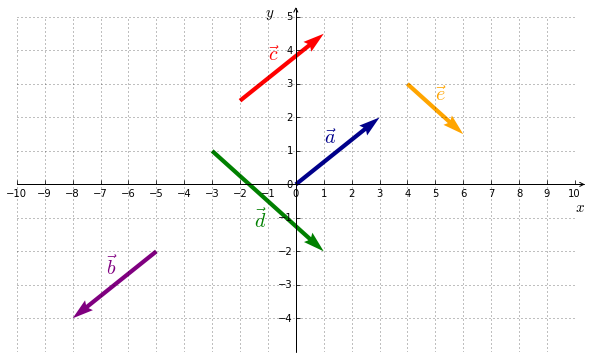
En référence à la Figure 5.1, on a :

${\color{navy}{\vec{a}}}$ et ${\color{red}{\vec{c}}}$ sont égaux. $\, {\color{navy}{\vec{a}}} ={\color{red}{\vec{c}}}$. Les coordonnées sont : ${\color{red}{\vec{c}}}=\left( \begin{smallmatrix} 3 \\ 2 \end{smallmatrix} \right)$.
${\color{navy}{\vec{a}}}$ et ${\color{purple}{\vec{b}}}$ ont la même direction, la même longueur mais de sens opposé. $\, {\color{navy}{\vec{a}}} =-{\color{purple}{\vec{b}}}$.
${\color{green}{\vec{d}}}$ et ${\color{orange}{\vec{e}}}$ ont la même direction, le même sens, mais pas la même longueur. $\, {\color{green}{\vec{d}}} =2\,{\color{orange}{\vec{e}}}$.

Figure 5.1 : vecteurs dans $\mathbb{R}^2$

2. Addition

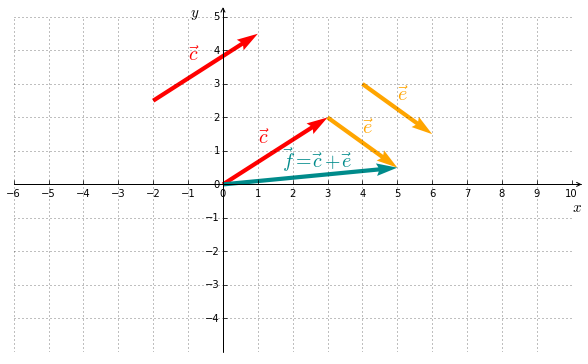
L’addition de vecteurs est définie comme suit :

$\begin{equation} \vec{a} + \vec{b} = \begin{pmatrix} a_1 \\ \vdots \\ a_n \end{pmatrix} + \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ \vdots \\ a_n + b_n \end{pmatrix} = \begin{pmatrix} b_1 + a_1 \\ \vdots \\ b_n + a_n \end{pmatrix} = \vec{b} + \vec{a} \end{equation}$

Géométriquement, la somme de deux vecteurs s’obtient en mettant les vecteurs bout à bout, tel qu’illustré à la Figure 5.2. On appelle cela la règle du parallélogramme.

Exemple I

Figure 5.2 : addition de vecteurs dans $\mathbb{R}^2$

$\begin{equation} {\color{darkcyan}{\vec{f}}} = {\color{red}{\vec{c}}} + {\color{orange}{\vec{e}}} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + \begin{pmatrix} 2 \\ -1.5 \end{pmatrix} = \begin{pmatrix} 5 \\ 0.5 \end{pmatrix} \end{equation}$

3. Soustraction

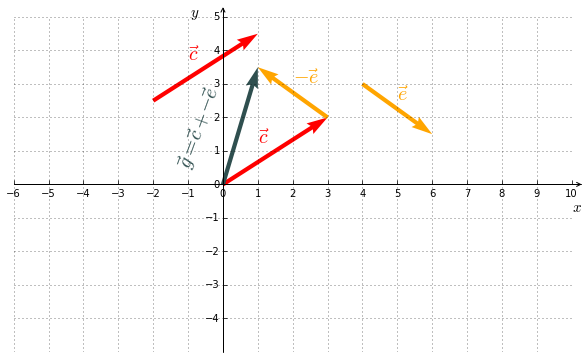
La soustraction d’un vecteur n’est rien d’autre que l’addition d’un vecteur dont on inverse le sens.

Exemple II

Figure 5.3 : soustraction de vecteurs dans $\mathbb{R}^2$

$\begin{equation} {\color{darkslategrey}{\vec{g}}} = {\color{red}{\vec{c}}} - {\color{orange}{\vec{e}}} = {\color{red}{\vec{c}}} + - {\color{orange}{\vec{e}}} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + -1\begin{pmatrix} 2 \\ -1.5 \end{pmatrix} = \begin{pmatrix} 1 \\ 3.5 \end{pmatrix} \end{equation}$

4. Multiplication par un scalaire (nombre)

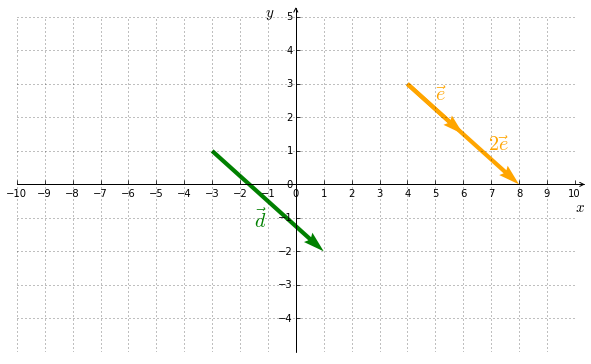
La multiplication d’un vecteur par un nombre donne un nouveau vecteur. Elle est définie comme suit :

$\begin{equation} \lambda \vec{v} = \lambda \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} \lambda v_1 \\ \vdots \\ \lambda v_n \end{pmatrix} \end{equation}$

Exemple III

Figure 5.4 : multiplication par un scalaire dans $\mathbb{R}^2$

$\begin{equation} {\color{green}{\vec{d}}} = 2 {\color{orange}{\vec{e}}} = 2 \begin{pmatrix} 2 \\ 1.5 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} \end{equation}$

Récapitulation

Géométriquement, un vecteur est une flèche qui a une direction, un sens et une longueur. Deux vecteurs sont égaux s’ils ont ces mêmes caractéristiques ou, en d’autres termes, s’ils ont les mêmes coordonnées.

Géométriquement, on peut voir un vecteur comme un point. La notion de vecteur généralise la notion de point.

Deux vecteurs qui ont la même direction s’expriment l’un en fonction de l’autre, tels que $\vec{d}$ et $\vec{e}$ dans la Figure 5.4. On dit qu’ils sont colinéaires ou, plus généralement, linéairement dépendants.

De manière plus générale, un vecteur est un concept algébrique et abstrait qui ne sera pas abordé dans le présent cours.