studybyyourself » Chapter 5 : Vector

1. Definition

Geometrically, a vector is an arrow having the three following characteristics :

a direction (the line that contains it)
a sense (top, right, bottom, left)
a length (also called norm)

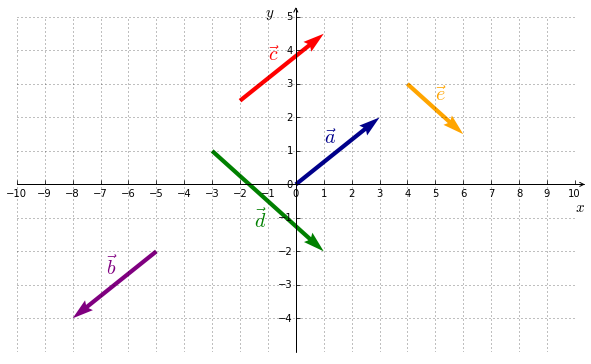
In Figure 5.1, we have the following :

${\color{navy}{\vec{a}}}$ et ${\color{red}{\vec{c}}}$ are equal. $\, {\color{navy}{\vec{a}}} ={\color{red}{\vec{c}}}$ . The coordinates are : ${\color{red}{\vec{c}}}=\left( \begin{smallmatrix} 3 \\ 2 \end{smallmatrix} \right)$ .
${\color{navy}{\vec{a}}}$ et ${\color{purple}{\vec{b}}}$ have the same direction, the same length but an opposite sense. $\, {\color{navy}{\vec{a}}} =-{\color{purple}{\vec{b}}}$ .
${\color{green}{\vec{d}}}$ et ${\color{orange}{\vec{e}}}$ have the same direction, the same sense, but a different length. $\, {\color{green}{\vec{d}}} =2\,{\color{orange}{\vec{e}}}$ .

Figure 5.1 : vectors in

$\mathbb{R}^2$

2. Addition

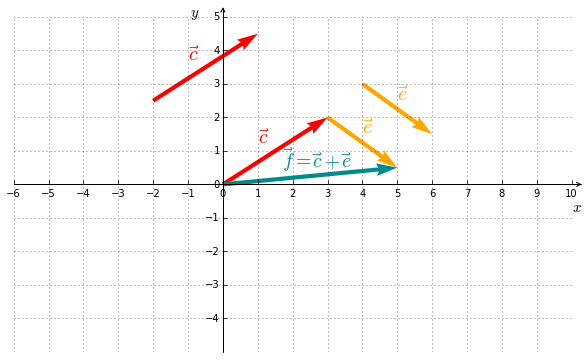
The addition of two vectors is defined as follows :

$\begin{equation} \vec{a} + \vec{b} = \begin{pmatrix} a_1 \\ \vdots \\ a_n \end{pmatrix} + \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ \vdots \\ a_n + b_n \end{pmatrix} = \begin{pmatrix} b_1 + a_1 \\ \vdots \\ b_n + a_n \end{pmatrix} = \vec{b} + \vec{a} \end{equation}$

Geometrically, the sum of two vectors is obtained by putting them end to end, as showed in Figure 5.2. This is the so-called parallelogram law.

Example I

Figure 5.2 : vector addition in

$\mathbb{R}^2$

$\begin{equation} {\color{darkcyan}{\vec{f}}} = {\color{red}{\vec{c}}} + {\color{orange}{\vec{e}}} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + \begin{pmatrix} 2 \\ -1.5 \end{pmatrix} = \begin{pmatrix} 5 \\ 0.5 \end{pmatrix} \end{equation}$

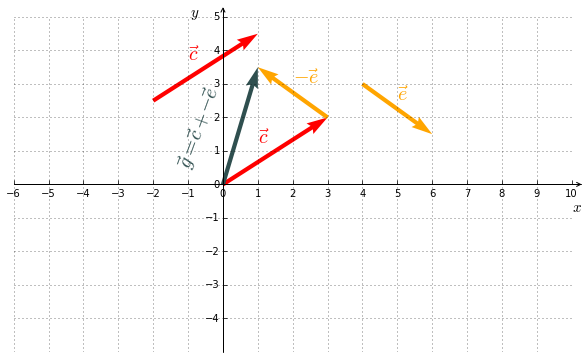
3. Subtraction

The vector subtraction is nothing but adding a vector whose sense is reversed.

Example II

Figure 5.3 : vector subtraction in

$\mathbb{R}^2$

$\begin{equation} {\color{darkslategrey}{\vec{g}}} = {\color{red}{\vec{c}}} - {\color{orange}{\vec{e}}} = {\color{red}{\vec{c}}} + - {\color{orange}{\vec{e}}} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + -1\begin{pmatrix} 2 \\ -1.5 \end{pmatrix} = \begin{pmatrix} 1 \\ 3.5 \end{pmatrix} \end{equation}$

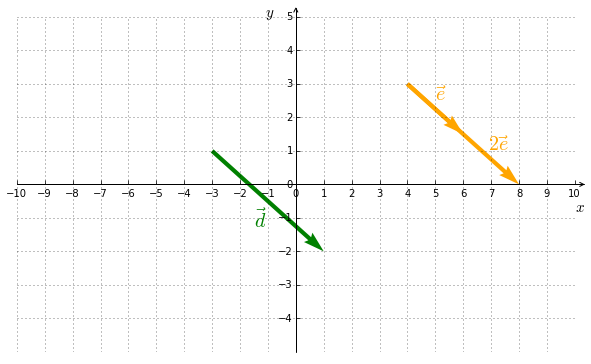
4. Multiplication by a scalar (number)

A vector multiplied by a scalar gives another vector. It is is defined as follows :

$\begin{equation} \lambda \vec{v} = \lambda \begin{pmatrix} v_1 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} \lambda v_1 \\ \vdots \\ \lambda v_n \end{pmatrix} \end{equation}$

Example III

Figure 5.4 : multiplication by a scalar in

$\mathbb{R}^2$

$\begin{equation} {\color{green}{\vec{d}}} = 2 {\color{orange}{\vec{e}}} = 2 \begin{pmatrix} 2 \\ 1.5 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} \end{equation}$

Recapitulation

Geometrically, a vector is an arrow having a direction, a sense and a length. Two vectors are equal if they have those same characteristics or, in other words, if they have the same coordinates.

Geometrically, a vector can been seen as a point. The concept of vector generalizes the concept of point.

If two vectors have the same direction, then they are multiples of one another, like $\vec{d}$ and $\vec{e}$ in Figure 5.4. In that case, they are said to be collinear or, more generally, linearly dependant.

More generally, a vector is an algebraic and abstract concept which is beyond the scope of the present course.