Chapitre 10 : Matrice inverse

1. Analogie

En algèbre basique, la solution de l’équation suivante est appelée l’inverse :

$$\begin{equation} ax = 1 \end{equation}$$

La solution de $(1)$ est $\frac{1}{a}$ qu’on écrit aussi $a^{-1}$.

En algèbre linéaire, l’équivalent de $(1)$ donne :

$$\begin{equation} AA^{-1} = I \end{equation}$$

Dans $(2)$, $I$ est appelée la matrice identité. Elle est composée de $1$ sur sa diagonale et le reste par des $0$, comme cela : $\left( \begin{smallmatrix} 1 & \cdots & 0 \\ \vdots & \phantom{/} 1 & \vdots \\ 0 & \cdots & 1 \end{smallmatrix} \right)$.

2. Calcul

La matrice inverse de $A=\left(
\begin{smallmatrix}
a_{1,1} & \cdots & a_{1,n} \\
\vdots & \cdots & \phantom{1}\vdots \\
a_{n,1} & \cdots & a_{n,n}
\end{smallmatrix}
\right)$ s’obtient en divisant la matrice transposée des cofacteurs, notée $C^{T}$, par le déterminant de $A$ :

Il y a dans $(3)$ deux concepts nouveaux. Premièrement, la matrice des cofacteurs (ou comatrice), deuxièmement la matrice transposée.

Commençons par expliquer comment transposer une matrice. Transposer une matrice revient à convertir ses lignes en colonnes.

Exemple I

Soit $A=\left( \begin{smallmatrix} -5 & 0 \\ -8 & -1 \end{smallmatrix} \right)$. Calculons sa transposée.

$$\begin{equation} \left( \begin{smallmatrix} -5 & 0 \\ -8 & -1 \end{smallmatrix} \right)^T = \left( \begin{smallmatrix} -5 & -8 \\ 0 & -1 \end{smallmatrix} \right) \end{equation}$$

Voyons maintenant la matrice des cofacteurs. Le cofacteur $c_{i,j}$ de $a_{i,j}$ est défini comme suit :

Dans $(5)$, $D_{i,j}$ est le déterminant de $A$ sans la ligne $\textbf{i}$ et sans la colonne $\textbf{j}$.

Exemple II

Soit $A=\left( \begin{smallmatrix} -5 & 0 \\ -8 & -1 \end{smallmatrix} \right)$. Calculons le $D_{1,2}$ de $A$.

$$D_{\color{orangered}{1},\color{orangered}{2}} = \begin{vmatrix} \enclose{horizontalstrike}{-5} & \enclose{horizontalstrike}{\color{orangered}{0}} \\ -8 & \enclose{horizontalstrike}{-1} \end{vmatrix} = \begin{vmatrix} -8 \end{vmatrix} = -8$$

Exemple III

Soit $A=\left( \begin{smallmatrix} 2 & 1 \\ 5 & -1 \end{smallmatrix} \right)$. Calculons son inverse.

Commençons par calculer son déterminant :

$$\begin{equation} \det(A) = \begin{vmatrix} 2 & 1 \\ 5 & -1 \end{vmatrix} = 2\cdot -1-5\cdot 1=-7 \end{equation}$$

Calculons maintenant la matrice des cofacteurs :

$$\begin{equation} C = \left( \begin{array}{} (-1)^{(1+1)}\begin{vmatrix} -1 \\ \end{vmatrix} & (-1)^{(1+2)}\begin{vmatrix} 5 \\ \end{vmatrix} \\ (-1)^{(2+1)}\begin{vmatrix} 1 \\ \end{vmatrix} & (-1)^{(2+2)}\begin{vmatrix} 2 \\ \end{vmatrix} \end{array} \right) = \left( \begin{array}{} -1 & -5 \\ -1 & 2 \end{array} \right) \end{equation}$$

On transpose $C$ et on peut obtenir la matrice inverse de $A$:

3. Fonction inverse

De manière plus générale, on peut voir la matrice inverse comme une fonction inverse.

En analyse, une fonction inverse, notée $f^{-1}$, permet de revenir sur le point de départ, comme l’illustre la Figure 10.1.

Or, une fonction $f$ a une inverse seulement si elle est bijective.

Figure 10.1 : fonction inverse (wikipedia)

Figure 10.2 : Bijection

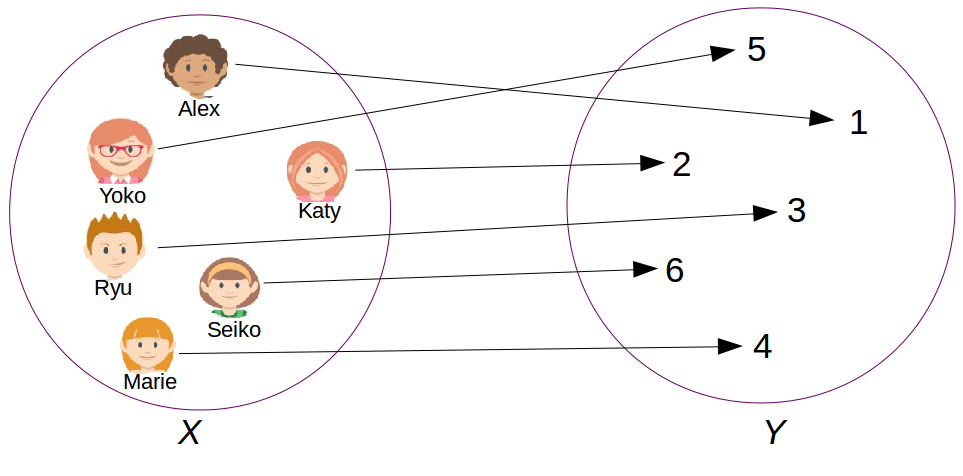
Une bijection est une fonction qui a une propriété particulière.
Chaque élément de l’ensemble de départ est associé, par la fonction, à un unique élément de l’ensemble d’arrivée et réciproquement. La Figure 10.2 illustre cette propriété.

Exemple IV

Soit $t$ :

$$\begin{equation} t \colon \, \mathbb{R}^2 \to \mathbb{R}^2 \\ \left( \begin{smallmatrix} x_1 \\ x_2 \end{smallmatrix} \right) \mapsto \left( \begin{smallmatrix} 2 & 1 \\ -6 & -3 \end{smallmatrix} \right) \left( \begin{smallmatrix} x_1 \\ x_2 \end{smallmatrix} \right) \end{equation}$$

$t$ n’est pas bijective car plusieurs $\vec{x}$ qui sont associés à $\vec{y}=\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix} \right)$.
En effet, si on décompose, $x_1
\left( \begin{smallmatrix} 2 \\ -6 \end{smallmatrix} \right) + x_2 \left( \begin{smallmatrix} 1 \\-3 \end{smallmatrix} \right) =
\left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix} \right)$ a une infinité de solutions car les vecteurs sont linéairement dépendants.

Récapitulation