studybyyourself » Chapter 8 : Basis

1. Analogy

Generally speaking, a base is a reference system in which things are expressed. For example, the number $64$ is written 1000 in the base $2$ (binary base). They are in fact the same number but they are expressed (represented) in different bases :

$\begin{equation} 64_{10} = 1000_{2} \end{equation}$

The natural base for numbers is the base 10. As regards vectors, the natural base is called the standard basis (also called canonical basis or normal basis).

2. Representations

As for numbers, vectors are represented with respect to a basis.

Example I

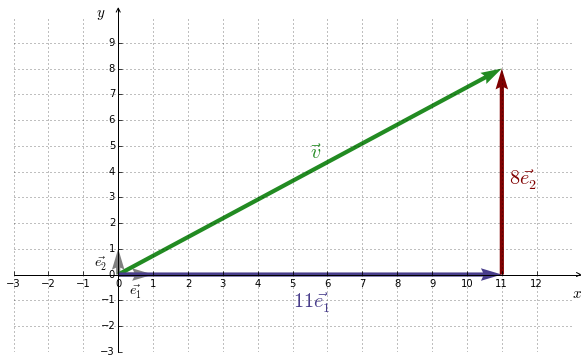
Figure 8.1 shows the vector $\vec{v}= \left( \begin{smallmatrix} 11 \\ 8 \end{smallmatrix} \right)$ represented in the standard basis of $\mathbb{R}^2$, namely $STD = \{ \underbrace{\left( \begin{smallmatrix} 1 \\ 0 \end{smallmatrix} \right)}_\vec{e_1},
\underbrace{\left( \begin{smallmatrix} 0 \\ 1 \end{smallmatrix} \right)}_\vec{e_2} \}$.

In fact, $\vec{v}$ is the result of a linear combination of the basis vectors :

$\begin{equation} \vec{v} = 11 \underbrace{\begin{pmatrix} 1 \\ 0 \end{pmatrix}}_{\vec{e_1}} + 8 \underbrace{\begin{pmatrix} 0 \\ 1 \end{pmatrix}}_{\vec{e_2}} = \begin{pmatrix} 11 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 8 \end{pmatrix} = \begin{pmatrix} 11 \\ 8 \end{pmatrix} \end{equation}$

Figure 8.1 : $\vec{v}$ in the standard basis of $\mathbb{R}^2$

Figure 8.2 : $\vec{v}$ in a given basis

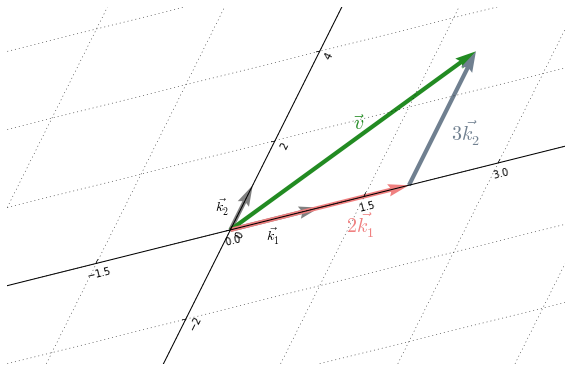
Let $B= \{ \underbrace{ \left( \begin{smallmatrix} 4 \\ 1 \end{smallmatrix} \right)}_{\vec{k_1}}
\underbrace{ \left( \begin{smallmatrix} 1 \\ 2 \end{smallmatrix} \right) }_{\vec{k_2}} \}$ be a basis of $\mathbb{R}^2$. Let’s represent $\vec{v}$ in $B$.

For doing that, we need to solve the following equation :

$\begin{equation} \vec{v} =\begin{pmatrix} 11 \\ 8 \end{pmatrix} = \lambda_1\vec{k_1} +\lambda_2\vec{k_2} = \lambda_1 \begin{pmatrix} 4 \\ 1 \end{pmatrix} + \lambda_2 \begin{pmatrix} 1 \\ 2 \end{pmatrix} \end{equation}$

In $(3)$ the coefficients $\lambda_i$ are the so-called components (also called coordinates). By solving $(3)$ we get $2$ and $3$ as components of $\vec{v}$ with respect to $B$.

Figure 8.2 shows $\vec{v}$ in $B$.

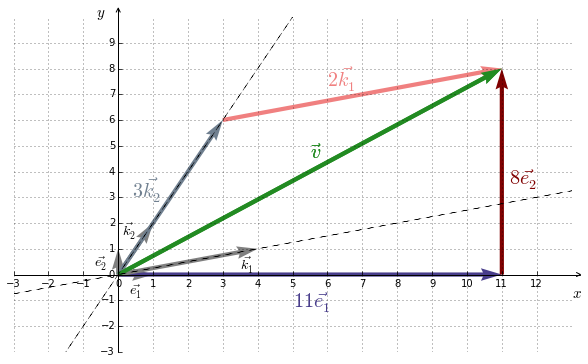
We have thus the vector $\vec{v}$ represented in two different basis :

$\begin{equation} \begin{pmatrix} 11 \\ 8 \end{pmatrix}_{STD} =\begin{pmatrix} 2 \\ 3 \end{pmatrix}_{B} \end{equation}$

Figure 8.3 : $\vec{v}$ in two different basis

3. Conditions

For being a basis the following conditions have to be met :

Any vector of a given space must be constructed from a linear combination of the basis vectors. That is the goal of a basis.
The vectors of the basis must be linearly independent.

4. Change of basis

To convert a vector from a given basis $B$ into the standard basis, the following formula can be used :

$\begin{equation} B \cdot \vec{v}_{B}= \vec{v}_{STD} \end{equation}$

Example II

Let’s convert $\vec{v}=\left( \begin{smallmatrix} 2 \\ 3 \end{smallmatrix} \right)$ from the basis $B=\{\left( \begin{smallmatrix} 4 \\ 1 \end{smallmatrix} \right),\left( \begin{smallmatrix} 1 \\ 2 \end{smallmatrix} \right)\}$, into the standard basis.

$\begin{equation} \begin{pmatrix} 4 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 11 \\ 8 \end{pmatrix} \end{equation}$

Recapitulation

Any vector is expressed with respect to a given basis. By default, vectors are expressed in the standard basis.

The standard basis of the space $\mathbb{R}^{2}$ is $\{ \left( \begin{smallmatrix} 1 \\ 0 \end{smallmatrix} \right),
\left( \begin{smallmatrix} 0 \\ 1 \end{smallmatrix} \right)
\}$. The standard basis of the space $\mathbb{R}^{3}$ is $\{ \left( \begin{smallmatrix} 1 \\ 0 \\ 0 \end{smallmatrix} \right),
\left( \begin{smallmatrix} 0 \\ 1 \\ 0 \end{smallmatrix} \right),
\left( \begin{smallmatrix} 0 \\ 0 \\ 1 \end{smallmatrix} \right)
\}$.

A basis of a given space generates, by linear combination, any vector of that space.

Are said to be the components (or coordinates) of a vector, the representation of a vector in a given basis.

All bases of $\mathbb{R}^{2}$ have $2$ vectors, all bases of $\mathbb{R}^{3}$ have $3$ vectors, etc. Generally speaking, all bases of $\mathbb{R}^{n}$ have $n$ vectors.