studybyyourself » Chapitre 12 : Diagonalisation

1. Analogie

Supposons qu’on désire faire un traitement numérique et qu’on veuille faire ce dernier dans la base la plus adaptée.

Prenons un exemple : on veut diviser un nombre paire par $2$. Il se trouve que la base la plus adaptée pour faire cela est la base binaire, car un simple décalage (shift) de gauche à droite fait ce traitement.

On a donc trois étapes :

Changement de base (de décimal à binaire)
On fait le traitement dans cette base (shift)
Changement de base (de binaire à décimal)

Exemple I

Divisons $208$ par $16$.

On procède par étapes comme vu plus haut :

Conversion de $208$ en base binaire : 11010000
1er shift : 01101000. 2e shift : 00110100. 3e shift : 00011010. 4e shift : 00001101
Conversion de 00001101 en base décimale : $13$

2. Calcul

Une matrice $A$ diagonalisable se décompose de la manière suivante :

$\begin{equation} A = P D P^{-1} \end{equation}$

Dans $(1)$ $P$ est la matrice des vecteurs propres de $A$ et $D$ la matrice des valeurs propres de $A$.

Dans notre analogie ci-dessus, le calcul de $A\vec{x}$ est traitement numérique à effectuer. On a donc en $(1)$, de droite à gauche :

Conversion de $\vec{x}$ dans une nouvelle base, noté $\vec{x}’$
Transformation linéaire dans la nouvelle base : $D\vec{x}’=\vec{y}’$
Conversion $\vec{y}’$ dans la base de départ, noté $\vec{y}$

Exemple II

Soit la matrice $A=\left( \begin{smallmatrix} 2 & 1 \\ 3 & 4 \end{smallmatrix} \right)$. Diagonalisons $A$.

Nous avons calculé les vecteurs propres de $A$ dans le chapitre consacré (prenons $\beta=1$).

Donc $P=\left( \begin{smallmatrix} 1 & 1 \\ -1 & 3 \end{smallmatrix} \right)$ et $P^{-1}= \frac{1}{4}\left( \begin{smallmatrix} 3 & -1 \\ 1 & 1 \end{smallmatrix} \right).$ La matrice des valeurs propres est : $D=\left( \begin{smallmatrix} 1 & 0 \\ 0 & 5 \end{smallmatrix} \right)$.

La diagonalisation de $A$ est donc :

$\begin{equation} \begin{pmatrix} 2 & 1 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 5 \end{pmatrix} \frac{1}{4} \begin{pmatrix} 3 & -1 \\ 1 & 1 \end{pmatrix} \end{equation}$

3. Concrètement ?

L’idée de la diagonalisation est d’effectuer la transformation linéaire dans une nouvelle base, plus appropriée. Cette base est composée des vecteurs propres et constitue un nouveau système d’axes.

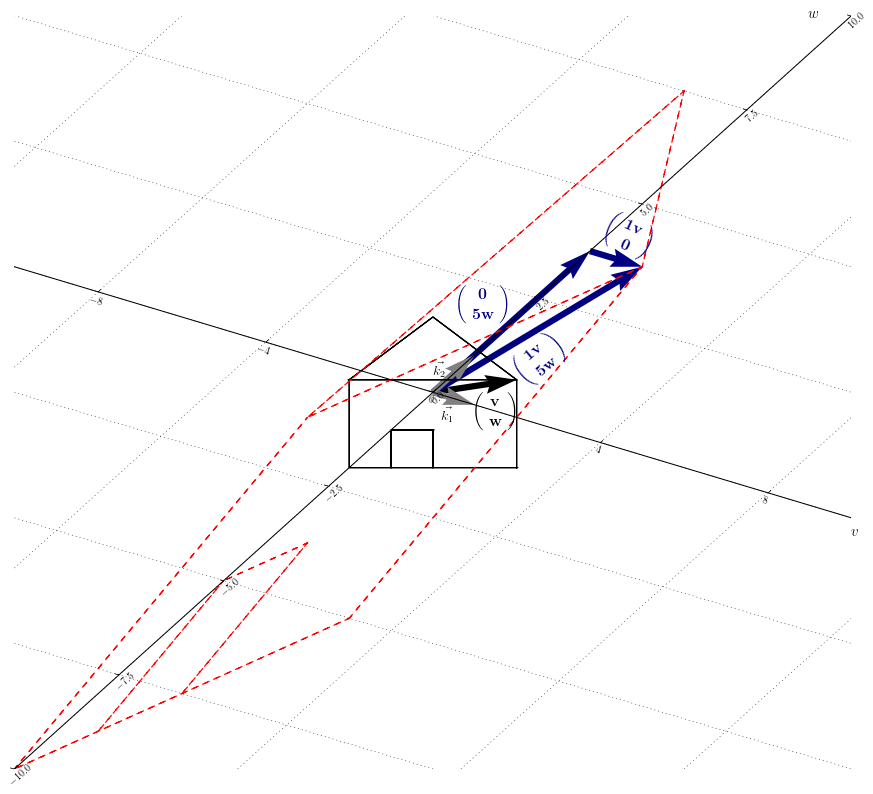
Ceci réduit les calculs, car dans la nouvelle base, $\vec{y}’$ s’obtient en multipliant par un facteur $\lambda_i$ les composantes de $\vec{x}’$, pour chaque axe de manière indépendante. La Figure 12.1 illustre la transformation linéaire de l’exemple II : $D \underbrace{ \left( \begin{smallmatrix} v \\ w \end{smallmatrix} \right) }_{\vec{x}’}
= \underbrace{\left( \begin{smallmatrix} 1v \\ 5w \end{smallmatrix} \right)
}_{\vec{y}’}$.

Figure 12.1 : application linéaire dans une nouvelle base

Récapitulation

La diagonalisation opère un changement de base. La nouvelle base est formée des vecteurs propres, pour autant que ceux-ci existent et qu’ils forment une base.

Une matrice $A$ diagonalisable se décompose comme suit :

$A = P D P^{-1}$

Chaque valeur propre dans $D$ doit être positionnée dans la même colonne que le vecteur propre correspondant dans $P$.

$D$ est une matrice diagonale. A cause des valeurs nulles en dehors de sa diagonale, $D$ agit sur chaque axe de manière indépendante, ce qui réduit les calculs.