Chapter 11 : Eigenvalues and eigenvectors

1. Definition

We have seen that a matrix $A$ multiplying a vector $\vec{x}$ is in fact a linear transformation.

We now are interested in the vector $\vec{x}$ whose image  $\vec{y}$ (under the linear transformation) is linearly dependent on itself, namely :

$\lambda$ and $\vec{x}$ satisfying $(1)$ are called respectively eigenvalues and eigenvectors.

In $(1)$ $\boldsymbol{\vec{0}}$ is excluded. Indeed we know anyway that $\underbrace{A\,\vec{0}}_{ \vec{0} }
= \underbrace{ \lambda\, \vec{0} }_{ \vec{0} } \,$ is true for any value of $\lambda$.

2. Calculation

From $(1)$ we can obtain :

$$\begin{equation} A\vec{x} = \lambda \vec{x} \iff A\vec{x}-\lambda \vec{x} = \vec{0} \iff (A -\lambda I)\,\vec{x} = \vec{0} \end{equation}$$

$$\begin{equation} \iff \left[ \left( \begin{array}{} a_{1,1} & \cdots & a_{1,n} \\ \phantom{1} \vdots & a_{i,i} & \phantom{1}\vdots \\ a_{n,1} & \cdots & a_{n,n} \end{array} \right) - \left( \begin{array}{} \lambda & \cdots & 0 \\ \vdots & \lambda & \vdots \\ 0 & \cdots & \lambda \end{array} \right) \right] \vec{x} = \vec{0} \end{equation}$$

$$\begin{equation} \iff \left( \begin{array}{} a_{1,1} -\lambda & \phantom{11} \cdots & a_{1,n} \\ \phantom{-11} \vdots & a_{i,i}-\lambda & \phantom{11}\vdots \\ \smash{ \underbrace{ a_{n,1} \phantom{1-\lambda}}_{ \vec{C_1} }} & \smash{ \underbrace{ \phantom{11} \cdots \phantom{1 \lambda} }_{ \vec{C_i} }} & \smash{ \underbrace{a_{n,n}-\lambda \phantom{1} }_{ \vec{Cn} }} \end{array} \right) \left( \begin{array}{} x_{1} \\ \vdots \\ x_{n} \end{array} \right) = \vec{0} \end{equation}$$

$$\begin{equation} \iff x_1 \vec{C_1} + \cdots + x_i \vec{C_i} + \cdots + x_n\vec{C_n} = \vec{0} \end{equation}$$

In $(5)$, the multiplication matrix by vector of $(4)$ has been decomposed. The columns $\vec{C_1}, \dots, \vec{C_n}$ must be linearly dependent since the $x_i$ cannot equal zero because of $(1)$. Therefore their determinant equals zero.

Once the $\lambda$’s (eigenvalues) are found by solving the determinant, we replace them in the matrix in $(4)$ to determine the associated eigenvectors.

Example I

Let $h$ : $h \colon \, \mathbb{R}^2 \to \mathbb{R}^2$, $ \vec{x} \mapsto \left( \begin{smallmatrix} 2 & 1 \\ 3 & 4 \end{smallmatrix} \right) \vec{x}$.
Let’s determine its eigenvalues and eigenvectors.

Based on $(4)$, we have :

$$\begin{equation} \left( \begin{array}{} 2-\lambda & 1 \\ 3 & 4-\lambda \end{array} \right) \vec{x} = \vec{0} \end{equation}$$

The columns of the matrix in $(6)$ are linearly dependent, thus :

$$\begin{equation} \begin{split} \begin{vmatrix} 2-\lambda & 1 \\ 3 & 4 -\lambda \\ \end{vmatrix} & = (2-\lambda)(4 -\lambda) -3 \\ & =8 - 2\lambda - 4\lambda +\lambda^2 -3 \\ & = \lambda^2 - 6\lambda + 5 \\ & = (\lambda-1)(\lambda-5) \\ & = 0 \end{split} \end{equation}$$

From $(7)$, we get : $\lambda_1 =1$ and $\lambda_2 =5$

To determine the eigenvector $\vec{x}_1$ associated to $\lambda_1$, we replace $\lambda_1$ in $(6)$ :

$$\begin{equation} \left( \begin{array}{} 2-1 & 1 \\ 3 & 4-1 \end{array} \right) \vec{x}_1 = \vec{0} \iff \left( \begin{array}{} 1 & 1 \\ 3 & 3 \end{array} \right) \vec{x}_1 = \vec{0} \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} 1 & 1 & 0 \\ 3 & 3 & 0 \end{array} \right) \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} 1 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \end{equation}$$

$ \iff 1x+1y = 0 \iff x=-y$.  Let $x= \beta$.

To determine the eigenvector $\vec{x}_2$ associated to $\lambda_2$, we replace $\lambda_2$ in $(6)$ :

$$\begin{equation} \left( \begin{array}{} 2-5 & 1 \\ 3 & 4-5 \end{array} \right) \vec{x}_2 = \vec{0} \iff \left( \begin{array}{} -3 & 1 \\ 3 & -1 \end{array} \right) \vec{x}_2 = \vec{0} \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} -3 & 1 & 0 \\ 3 & -1 & 0 \end{array} \right) \iff \left( \begin{array}{!{}l@{~} !{~}l | !{~}l@{}} -3 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \end{equation}$$

$ \iff -3x+1y = 0 \iff y=3x \iff x=\frac{y}{3}$.  Let $x= \beta$.

3. Visualization

Figure 11.1 : eigenvector and an ordinary vector

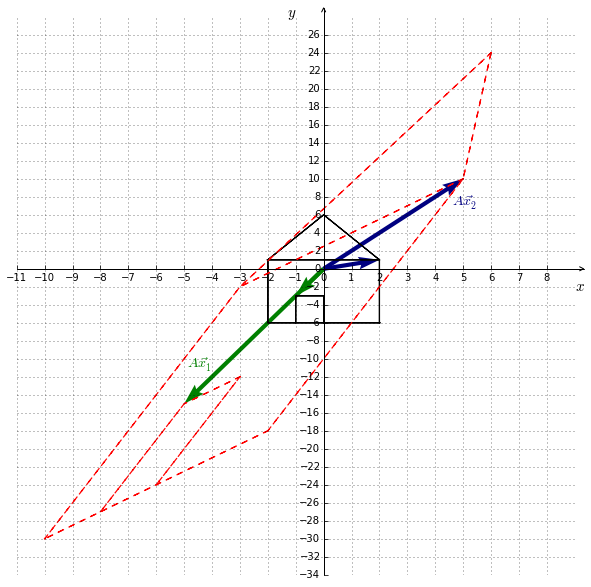
Figure 11.1 shows a shape before and after the transformation (in dashed lines) under the linear transformation of example I.

The eigenvector $\,\color{green}{\vec{x_1}}=\left(\begin{smallmatrix} -1 \\ -3 \end{smallmatrix}\right)$, as well as the ordinary vector   $\color{navy}{\vec{x_2}}=\left(\begin{smallmatrix} 2 \\ 1 \end{smallmatrix}\right)$ are represented too. The eigenvector does not rotate under the linear transformation.

Wrap-up